Pr Byesian Nn

17 Mar 2019

본 포스트는 다음의 post를 간단히 요약한 내용입니다.

https://medium.com/@joeDiHare/deep-bayesian-neural-networks-952763a9537

글쓴이는 neural network의 불확실성을 모델링하기 위해 3개의 bayesian approach를 제안한다.

1) MCMC integral의 근사화 2) black-box variational inference 3) MC dropout사용

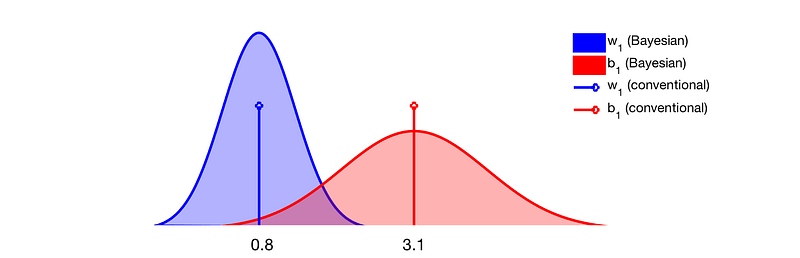
기존의 전통적인 방식은 likekihood 최대로하는 optimal value를 학습하는, 즉 weight와 bias를 예측하는 방법이었다. 이 경우 weight와 bias는 scalars 값을 가진다. 반면에, Bayesian approach는 이 파라미터들의 분포에 관한 것이다.

예를들어 앞선 weight와 bias는 학습이 완료된 네트워크가 가질수 있는 값드의 분포로 표현될 수 있다. 나의 해석으로는 네트워크가 학습될 수 있는 local minima가 엄청나게 많은데 그 값들이 분포를 가짐을 의미한다고 생각한다.

그렇다면 여기서 생각해볼 내용은, single value가 아닌 분포를 가진다는 것이 어떠한 장점이 있을까? 글쓴이는 이를 당연하게 분포의 관점에서 설명한다. 즉, 분포의 의미인 샘플링을 거듭하여 학습하였을 경우에 지속적으로 같은 예측을 한다면 그 결과는 신뢰할만 하다는 내용이다.

다시 분포로 돌아가면, 문제는 deep neural network란 다음의 posterior pdf를 찾는 문제로 볼 수 있다. 여기서 posterior는 당연하게도 우리가 아는 Bayes rule을 통해서 얻어진다.

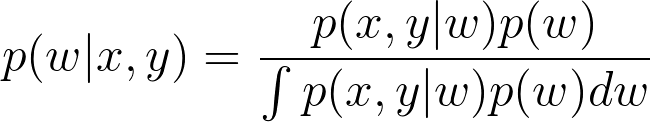
위의 식에서 가장 문제는 당연히 분모 P(x,y) 이다. 왜냐하면 수식에서 처럼, 모든 weight 파라미터에 대해서 이 확률을 다 구하는 것은 불가능에 가깝기 때문이다. 결국 exhaustive search인데 가능하겠는가?

결국 Deep Bayesian Neural Network 방식은 이 분모를 근사화시켜서 푸는 방식을 이야기하는 것이다.

먼저 방안 1은 Markov Chain MonteCarlo를 사용하는 것이다. 사실 나는 Markov chain과 MonteCarlo 각각은 당연히 엄청나게 많이 들어봤지만, 이 둘을 결합한 방식은 처음 들어보았다. 하지만 내가 짧게 공부하기론 그냥 그 둘은 섞은 방식으로 이해했다. 즉 Markov chain은 state와 trainsiotion이 정의 되고 이들을 확률로 표현한 모델을 이야기하는데, 이렇게 표현된 모델을 MonteCarlo 방식으로 확률을 구한 것이다. 좀 더 딥러닝 관점에서 생각해 보자면, 네트워크거 여러 계층으로 구성되는 상황에서 각 계층을 state로 표현하고 state간 이동인 weight를 trainsition으로 표현하는 것이라고 이해하면 될 듯하다. 즉, posterior probability를 DnC하여 푸는 방식이라고 생각하면 편할 듯하다.

다음으로 글쓴이가 설명한 Byesian NN을 근사화하는 2번째 방법은 black-box variation inference이다.

먼저 variation inference 정의를 살펴보면

Variational inference is an approach to estimate a density function by choosing a distribution we know (eg. Gaussian) and progressively changing its parameters until it looks like the one we want to compute, the posterior. Variational inference is an approach to estimate a density function by choosing a distribution we know (eg. Gaussian) and progressively changing its parameters until it looks like the one we want to compute, the posterior.